To plot the graph of the function:
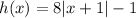
According to your graphing software, we need to find the smallest value of the function, and any point at the positive slope side of the function. Let's start with the minimum point. Let's use the general formula for an absolute value function:

The coefficients 'b' and 'c' determinates how much the function was translated from the origin. The 'b' determinates in the x-axis, and the 'c' determinates in the y-axis.
If the 'b' is positive, the function translated to the left, if it is negative the function translated to the right.
If the 'c' is positive the function went up, and if it is negative it went down.
Now let's analyze our h(x) function. Our coefficients are:
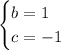
Which means our minimum point is
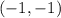
Now, we just need to calculate any point to the right of x = -1.
Let's calculate for x = 0.

The second point is (0,7)