Given the circle G
As shown, m∠FGH = 36
And the radius of the circle = r = FG = 10 units
we will find the length of the arc FH using the formula:
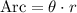
The given angle measured in degree, we will convert it to radian
So,
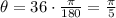
So, the length of the arc =
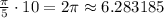
Round to the nearest hundredth.
So, the answer will be the length of the arc FH = 6.28