We will investigate some application of line bisectors.
We have a line segment denoted as ( CR ). A point ( A ) is said to be bisecting the line segment.
Line bisection involves the process of equally dividing the entire line segment in two equal halves! We can also represent this scenario graphically for clearification:
We can also represent line bisection mathematically in terms of two smaller divisions ( CA and AR ) as follows:
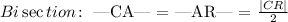
Where, the quantities are expressed as magnitudes/lengths of each segment indicated.
We are given expressions for bifurcated line segments |CA| and |AR| in terms of variable ( x) as follows:
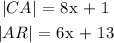
Now we will use the expression given for each smaller division of line |CR| and plug it in the general " Bisection " expression developed above:
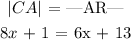
We have constructed an equation with a single variable ( x ). We can solve this equation for the variable ( x ) using basic mathematical operations as follows:
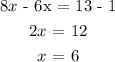
Once we have solved for the variable ( x ). We will again use the defined expression for each smaller segments and determine the magnitudes as follows:
