Given,
The weight of the student, W=500 N
Thus the mass of the student is given by,
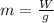
Where g is the acceleration due to gravity,
On substituting the known values,
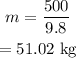
For the first 5 seconds, the net force acting on the student is 0 N. Thus scale reads only his weight. As the net force is zero the acceleration of the elevator is also zero.
In the next 5 intervals, the net force acting on the student is F=200 N, as seen from the diagram.
Thus the acceleration of the elevator is given by the equation,
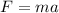
Where a is the acceleration of the elevator.
On substituting the known values,
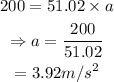
Thus the acceleration in this interval is 3.92 m/s²
During the interval, 10s-15s, the net force acting on the student is zero as seen from the graph. Thus the acceleration of the elevator is also zero.
During the interval, 15 s-20 s, the net force on the student is F=-200 N as seen from the diagram.
Thus the acceleration is,
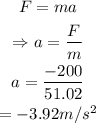
Thus the accelerating in this interval is -3.92 m/s²That is the elevator is accelerating downwards.