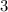The question is to evaluate the quotient and remainder of the division using the long division method:
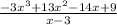
Step 1: Write out the problem in the long division format
Step 2: Divide the leading term of the dividend by the leading term of the divisor. Write down the calculated result in the upper part of the table. Multiply it by the divisor and subtract the dividend from the obtained result
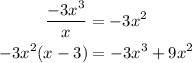
Step 3: Apply the steps from 2 above to the remainder at the bottom
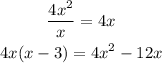
Step 4: Apply the steps from 3 above
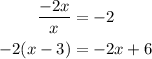
Step 5: Since the degree of the remainder is less than that of the divisor, we are done with the division. The quotient is the polynomial at the top and the remainder is at the bottom

ANSWER
The quotient is:
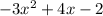
The remainder is