Take x and y as the two numbers, the sum of these is 24:
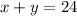
It is also stated that the second number, y, is 4 less than the first, x, it means:
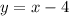
The system of equations is:
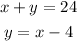
Use the second equation, which is solved for y and replace this expression for y in the first equation, then solve for x:
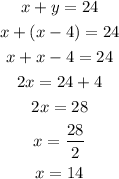
x has a value of 14. Use this value and the second equation to find the value of y:
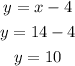
The solution for the system is (14,10). The correct answer is B.