Answer:
(9, 2)
Explanation:
What point divides the directed line segment AB¯¯¯¯¯ into a 3:1 ratio?
coordinate plane with segment A B with A at (0, 2) and B at (12, 2)
(3, 2)
(4, 2)
(8, 2)
(9, 2)
Solution:
If point O(x, y) divides the line segment AB with endpoints A(
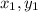 ) and B(
) and B(
 ) in the ratio n:m, the coordinates of O is:
) in the ratio n:m, the coordinates of O is:
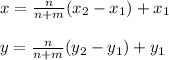
Let us assume C(x, y) is the point that divides segment A B with A at (0, 2) and B at (12, 2) in the ratio 3 : 1. Hence:

Therefore the coordinate of point C is at (9, 2).