Question

i was absent for the day we reviewed the question and my teacher won't help me understand. the image given is my problem.

Answer 1

Step 1. Find the coordinates of point D.

In this problem, we have a segment called CD with two endpoints. We know one of the endpoints:

`(2,-1)`

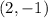
And we don't know the other endpoint, but we know the midpoint:

`(8,3)`

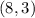
We will label these known points as the first point (x1,y1) and the midpoint (xm, ym) as follows:

`\begin{gathered} x_1=2 \\ y_1=-1 \\ x_m=8 \\ y_m=3 \end{gathered}`

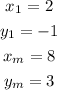
To find the second endpoint which we will call the second point (x2,y2) we use the midpoint formulas:

`\begin{gathered} x_m=(x_1+x_2)/(2) \\ y_m=(y_2+y_2)/(2) \end{gathered}`

Solving each equation respectively for x2 and y2:

`\begin{gathered} x_2=2x_m-x_1 \\ y_2=2y_m-y_1 \end{gathered}`

And substituting the known values for the first point and the midpoint:

`\begin{gathered} x_2=2(8)-2=16-2=14 \\ y_2=2(3)-(-1)=6+1=7 \end{gathered}`

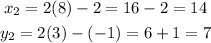
We have found the second endpoint (x2,y2):

`(14,7)`

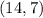
Step 2. Once we know the two endpoints of the segment CD:

`\begin{gathered} (2,-1) \\ \text{and} \\ (14,7) \end{gathered}`

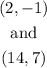
We make a graph for reference:

Note: the diagram is not to scale.

The length of the red line is what we are asked to find.

To find this length, draw a triangle between the points, shown here in green:

The triangle is a right triangle, this means we can use the Pythagorean theorem:

The Pythagorean theorem helps us find the hypotenuse ''x'' of the triangle when we know the legs a and b.

In this case, a and b are:

Substituting in the Pythagorean theorem:

`\begin{gathered} x=\sqrt[\square]{a^2+b^2} \\ x=\sqrt[]{12^2+8^2} \end{gathered}`

Solving the operations:

`\begin{gathered} x=\sqrt[]{144-64} \\ x=\sqrt[]{80} \\ x=8.9 \end{gathered}`

The solution is b. 8.9 units.

Answer: 8.9 units