The given function is:
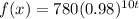
It is required to state what the constant 0.98 reveal about the rate of change of the quantity by completing the given statement:
The function is exponentially at a rate of every .
Notice from the given exponential function that the factor is 0.98.
Since it is less than 1, it implies that it is an exponential DECAY.
Subtract the factor 0.98 from 1 to get the decay rate:

Unit of t: decades
The exponent is 10t.
The reciprocal is 1/10.
Hence, the time frame of rate is: 1/10 of a decade.
This is equivalent to a year.
The complete statement is, therefore:
The function is decaying exponentially at a rate of 2% every year.