Answer:
The component form of the velocity of the airplane is
![\vec v = 389.711\,\hat{i} -225\,\hat{j}\,\left[(m)/(s) \right]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/vzjpbgkvoupvq33gs2fb5x.png) .
.
Explanation:
Let suppose that a bearing of 0 degrees corresponds with the
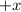 direction and that angle is measured counterclockwise. Besides, we must know both the magnitude of velocity (
direction and that angle is measured counterclockwise. Besides, we must know both the magnitude of velocity (
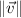 ), in miles per hour, and the direction of the airplane (
), in miles per hour, and the direction of the airplane (
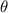 ), in sexagesimal degrees to construct the respective vector. The component form of the velocity of the airplane is equivalent to a vector in rectangular form with physical units, that is:
), in sexagesimal degrees to construct the respective vector. The component form of the velocity of the airplane is equivalent to a vector in rectangular form with physical units, that is:
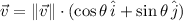 (1)
(1)
If we know that
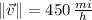 and
and
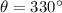 , then the component form of the velocity of the airplane is:
, then the component form of the velocity of the airplane is:
![\vec v = 389.711\,\hat{i} -225\,\hat{j}\,\left[(m)/(s) \right]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/vzjpbgkvoupvq33gs2fb5x.png)
The component form of the velocity of the airplane is
![\vec v = 389.711\,\hat{i} -225\,\hat{j}\,\left[(m)/(s) \right]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/vzjpbgkvoupvq33gs2fb5x.png) .
.