Answer
The answer is 0.300
Problem Statement
We are asked to find the probability that the number of individuals in a survey of 500 people would skip breakfast given that the proportion of people who skip breakfast, in general, is 0.238.
Method
- The proportion of people greater than 124 out of 500 is easily gotten to be:
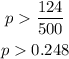
- We now need to know the probability that the proportion of people that skip breakfast would be greater than 0.248.
- To calculate this probability, we need to find the Z-score associated with this value. This is a good way to approximate the probability because the number of people in the survey is well above 30 and we have been told to apply a normal approximation.
- Once we have the Z-score associated with this proportion of 0.248 in relation to the general population proportion statistic of 0.238, we can then convert the Z-score into a probability using a Z-score calculator or a Z-table.
- If the Z-score is "z", then, the probability we are looking for on the Z-score table or calculator is P(x > z).
- Thus, we can solve the question using the following steps:
1. Calculate the Z-score using the formula below:
![\begin{gathered} z=\frac{p-p_0}{\sqrt[]{(p_0(1-p_0))/(n)}} \\ \\ \text{where,} \\ p=\text{sample proportion} \\ p_0=\text{population proportion} \\ n=\text{ Total number of people in the survey} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/fm8jqbbat63na0tlcmx5usullgl1pkifx8.png)
2. Convert the Z-score into probability
Implementation
Step 1: Calculate the Z-score:
![\begin{gathered} p=0.248,p_0=0.238 \\ \\ z=\frac{0.248-0.238}{\sqrt[]{(0.238(1-0.238))/(500)}} \\ \\ z=(0.01)/(0.019045) \\ \\ z=0.5251 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/uquxbsdjpeiqzwfr7zyqrc1bs752fkiyd0.png)
2. Convert the Z-score into probability:
Using the Z-score calculator, we have:
Because we are asked to find the probability that the number of people who skipped breakfast is greater than 124, the correct probability here is P(x > Z).
Thus, the probability that the number of individuals that skipped breakfast is greater than 124 is 0.29977 ≅ 0.300 (To 3 decimal places)
Final Answer
The answer is 0.300.