Given the following definite integral.
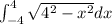
We will use the substitution to solve the definite integral
Let the following:
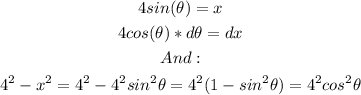
Substitute into the given integral:
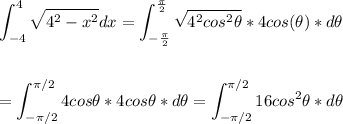
Now, we will use the following identity:
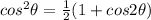
So, the integral will be:
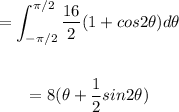
substitute θ = π/2, and θ = -π/2
So, the value of the integral =
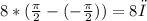
So, the answer will be: Area = 8π
The graph of the given function is shown in the following picture