Question

Car X weighs 136 pounds more than car Z. Car Y weighs 117 pounds more than car Z. The total weight of all three cars is 9439 pounds. How much does each car weigh?

Answer 1

Let x, y and z denote the weighs of car X, car Y and car Z, respectively.

We know that car X weighs 136 more than car Z, this can be express by the equation:

`x=z+136`

We also know that Y weighs 117 pounds more than car Z, this can be express as:

`y=z+117`

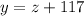
Finally, we know that the total weight of all the cars is 9439, then we have:

`x+y+z=9439`

Hence, we have the system of the equations:

`\begin{gathered} x=z+136 \\ y=z+117 \\ z+y+z=9439 \end{gathered}`

To solve the system we can plug the values of x and y, given in the first two equations, in the last equation; then we have:

`\begin{gathered} z+136+z+117+z=9439 \\ 3z=9439-136-117 \\ 3z=9186 \\ z=(9186)/(3) \\ z=3062 \end{gathered}`

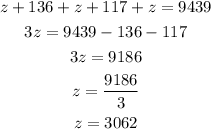
Now that we have the value of z we plug it in the first two equations to find x and y:

`\begin{gathered} x=3062+136=3198 \\ y=3062+117=3179 \end{gathered}`

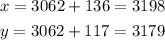
Therefore, car X weighs 3198 pound, car Y weighs 3179 pounds and car Z weighs 3062 pounds.