Question

A lottery offers one $900 prize, one $600 Prize, three $400 prizes, and four $100 prizes. One thousand tickets are sold at $5 each. Find the expectation if a person buys four tickets. Assume that the player's ticket is replaced after each draw and that the same ticket can win more than one prize. Round to two decimal places for currency problems.

Answer 1

Expected value for 4 tickets = $ -7.6

Explanation:

Given - A lottery offers one $900 prize, one $600 Prize, three $400 prizes, and four $100 prizes. One thousand tickets are sold at $5 each.

To find - Find the expectation if a person buys four tickets. Assume that the player's ticket is replaced after each draw and that the same ticket can win more than one prize. Round to two decimal places for currency problems.

Proof -

Given that,

A lottery offers

one $ 900 prize

one $ 600 prize

three $ 400 prizes

Four $ 100 prizes

And

One thousand tickets are sold at $ 5 each

Now,

If the person bought 1000 tickets then the prize he gets is

= 900 + 600 + 3×400 + 4×100

= 900 + 600 + 1200 + 400

= $3100

And

The cost of 1000 tickets = 5×1000 = $ 5000

Now,

Price 1 ticket =
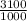`(3100)/(1000)` = $ 3.1

⇒Expectation of 1 ticket = $ 3.1 - 5 = $ -1.9 (Here $5 is price of 1 ticket)

⇒Expected value for 4 tickets = $ 4× -1.9 = $ -7.6

⇒Expected value for 4 tickets = $ -7.6