Answer:
V_{average} =
 , V_{average} = 2 V
, V_{average} = 2 V
Step-by-step explanation:
he average or effective voltage of a wave is the value of the wave in a period
V_average = ∫ V dt
in this case the given volage is a square wave that can be described by the function
V (t) =
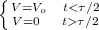
to substitute in the equation let us separate the into two pairs
V_average =
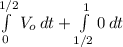
V_average =
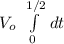
V_{average} =

we evaluate V₀ = 4 V
V_{average} = 4 / 2)
V_{average} = 2 V