Question

Solve this system of equations by graphing. First graph the equations, and then type the solution.x+3y=6y=1/2x+7

Answer 1

Given the system of equations;

`\begin{gathered} x+3y=6---(1) \\ y=(1)/(2)x+7---(2) \end{gathered}`

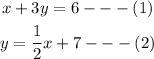
We shall first of all re-arrange the equations in the slope-intercept form;

`y=mx+b`

Note that the second one has already been expressed in the slope-intercept form. For the first one we would now have;

`\begin{gathered} x+3y=6 \\ 3y=-x+6 \\ \text{Divide both sides by 3;} \\ (3y)/(3)=-(x)/(3)+(6)/(3) \\ y=-(1)/(3)x+2 \end{gathered}`

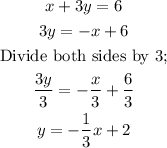
To plot this equations on a graph we take two extreme points. We can do this by finding the value of y when x = 0, and y when x = 0.

For the first equation, we would have;

`\begin{gathered} y=-(1)/(3)x+2 \\ \text{When x}=0 \\ y=-(1)/(3)(0)+2 \\ y=0+2 \\ y=2 \\ \text{That means we have the point }(0,2) \\ \text{Also, when y}=0 \\ 0=-(1)/(3)x+2 \\ (1)/(3)x=2 \\ \text{Cross multiply this and you'll have;} \\ x=2*3 \\ x=6 \\ We\text{ now have our second point, }(6,0) \end{gathered}`

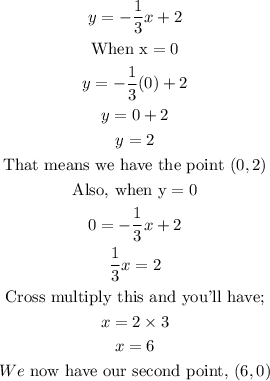
Hence, for the first equation we have the two points;

`\begin{gathered} A(0,2) \\ B(6,0) \end{gathered}`

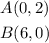
For the second equation;

`\begin{gathered} y=(1)/(2)x+7 \\ \text{When x}=0 \\ y=(1)/(2)(0)+7 \\ y=0+7 \\ y=7 \\ \text{This means we have the point }(0,7) \\ \text{Also, when y}=0 \\ 0=(1)/(2)x+7 \\ -(1)/(2)x=7 \\ \text{Cross multiply and you'll have;} \\ x=7*(-2) \\ x=-14 \\ \text{That means we now have the second point which is }(-14,0) \end{gathered}`

For the second equation we now have the points;

`\begin{gathered} A(0,7) \\ B(-14,0) \end{gathered}`

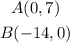
We can now input both sets of coordinates and our graph would come out as shown below.

The point of intersection as we can see is at where x = -6 and y = 4. Therefore;

ANSWER:

The solution to the system of equations as shown on the graph is;

`(-6,4)`