Solution:
From the given graphs,
The first graph is the absolute function graph.
Which can be expressed in the form
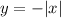
Since the leading coefficient is negative,
The end behavior of the graph is
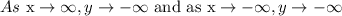
Hence, the answers are C and D
The second graph is a quadratic graph of the form
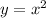
Since the leading coefficient is positive
The end behavior will be
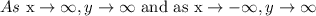
Hence, the answers are A and B
The third graph is a cubic function that can be expressed in the form
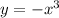
The leading coefficient is negative.
The end behavior will be
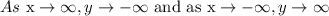
Hence, the answers are C and B