Answer:
3x+5y=12.
Step-by-step explanation:
Given the line: 5x-3y=2
First, we determine the slope by making y the subject of the equation.
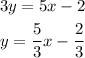
Comparing with the slope-intercept form: y=mx+b
• Slope = 5/3
Let the slope of the perpendicular line = n
By definition. two lines are perpendicular if the product of their slopes is -1.
Therefore:
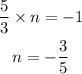
Next, we use the point-slope form to find the perpendicular to the given line that is passing through (-1, 3).
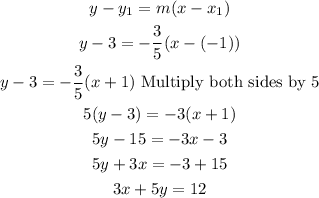
The required equation is 3x+5y=12.