Question

O is the center of the regular decagon below. Find its area. Round to the nearesttenth if necessary.

Answer 1

Since O is the center of the regular decagon, the area of this decagon is 355.7 square units.

In Mathematics and Geometry, the sum of the interior angles of both a regular and irregular polygon is given by this formula:

Sum of interior angles = 180 × (n - 2)

Note: The given geometric figure (regular polygon) represents an decagon and it has 10 sides.

For the central angle substended, we have;

x = 360°/10 ÷ 2.

x = 18°.

Next, we would determine the edge length as follows;

sin(18) = x/11

x = 11sin(18)

x = 3.4 units.

For the apothem, we have;

`a^2=11^2-3.4^2\\\\a=√(109.44)`

a = 10.461357464497616525368756761263 units.

Now, we can determine the area of this decagon as follows;

Area of polygon = (n × s × a)/2

Where:

• n is the number of sides.
• s is the side length.
• a is the apothem.

Area of decagon = (10 × 3.4 × 10.461357464497616525368756761263)/2

Area of decagon = 355.7 square units.

Answer 2

Step-by-step explanation:

Given;

We are given a decagon, which is a 10-sided polygon with center O, and a radius of 11 units.

Required;

We are required to find the area of the decagon and round the answer to the nearest tenth.

Step-by-step solution;

We begin by calculating the interior angle of e decagon.

We use the formula;

`\begin{gathered} S=(n-2)180 \\ Where: \\ S=sum\text{ }of\text{ }interior\text{ }angles \\ n=number\text{ }of\text{ }sides \end{gathered}`

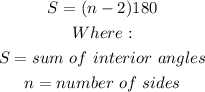
Therefore;

`\begin{gathered} S=(10-2)180 \\ \\ S=8*180 \\ \\ S=1440\degree \end{gathered}`

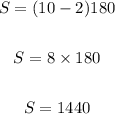
For a 10-sided polygon, each interior angle will now measure;

`\begin{gathered} Interior\text{ }angle=(1440)/(10) \\ \\ Interior\text{ }angle=144\degree \end{gathered}`

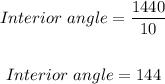
take note that the radius of the polygon divides the angle at the vertex (that is, the interior angle) into two equal halves.

With that in mind we can now construct the following triangle;

Take note that the line from the center to the side is the apothem, while the side labeled 11 is the radius (which was given). We can now extract one of the right angled triangles and use that calculate the apothem as follows;

The side labeled a, the apothem can be calculated using the angle 72 degrees as the reference angle;

`\begin{gathered} Reference\text{ }angle=72 \\ Opposite=a \\ Hypotenuse=11 \end{gathered}`

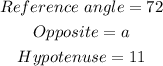
Note that;

`sin\theta=(opposite)/(hypotenuse)`
`sin72=(a)/(11)`

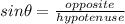
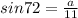
We cross multiply and we have;

`\begin{gathered} 11* sin72=a \\ \\ 10.46=a \end{gathered}`

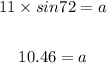
Also, for the side labeled s (half the length of one side of the decagon);

`cos\theta=(adjacent)/(hypotenuse)`

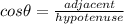
Therefore;

`cos72=(s)/(11)`

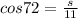
We cross multiply and we now have;

`\begin{gathered} 11* cos72=s \\ \\ 3.39=s \end{gathered}`

For the length of one side of the decagon, we have the side s times 2. Hence, the length of the side is

`\begin{gathered} Length\text{ }of\text{ }side=3.39*2 \\ \\ Length\text{ }of\text{ }side=6.78 \end{gathered}`

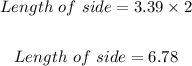
The area of a polygon is given by the formula;

`Area=(1)/(2)* a* p`

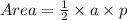
Where the variables are;

`\begin{gathered} a=apothem \\ p=perimeter \end{gathered}`
`\begin{gathered} Perimeter=6.78*10 \\ Perimeter=67.8 \end{gathered}`
`\begin{gathered} Area=(1)/(2)*10.46*67.8 \\ \\ Area=354.594 \end{gathered}`

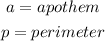
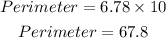
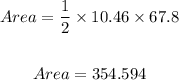
Therefore, the area of the decagon rounded to the nearest tenth is;

ANSWER:

`Area=354.594units^2`