Given,
The height at which the satellite was orbiting the moon, h=122 km=122×10³ m
The radius of the moon, R=1840×10³ m
The mass of the moon, m=7.3×10²² kg
a.
The orbital velocity of the Apollo 11 is given by,
![v=\sqrt[]{(GM)/(R+h)}](https://img.qammunity.org/2023/formulas/physics/college/k6xzmqpm223dfq8bdebbksf94w9a5rmcus.png)
Where G=6.67×10⁻¹¹ m³ kg⁻¹ s⁻² is the gravitational constant.
On substituting the known values,
![\begin{gathered} v=\sqrt[]{(6.67*10^(-11)*7.3*10^(22))/(1840*10^3+122*10^3)} \\ =1.58*10^3\text{ m/s} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/dhc995m8ck42vl5z9lkmzb9ktex9uycg71.png)
Thus the orbital speed of the spacecraft is 1.58×10³ m/s
b.
The time it takes for the spacecraft to orbit once is called the time period of the spacecraft.
The time period of the spacecraft is given by,
![T=2\pi\sqrt[]{((R+h)^3)/(GM)}](https://img.qammunity.org/2023/formulas/physics/college/zvgt1r1t98n9h0ahezymdhqtnr1gelpbgr.png)
On substituting the known values,

Converting the period to hours,
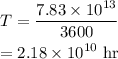
Thus the time it takes for the spacecraft to orbit once is 7.83×10¹³ s, that is 2.18×10¹⁰ hr