Question

For the sequence 25,22,19,16... find. A. formula for the nth term B. sum of the first 20 teams

Answer 1

Given:-

`25,22,19,16,\ldots`

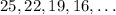
To find the nth term and the sum of first 20 terms.

So now we use the formula,

`T_n=a+(n-1)d`

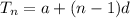
So the value of a is the first term 25 and the value of d is,

`d=22-25=-3`

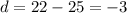
So the nth term is,

`T_n=25+(n-1)(-3)`

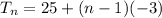
So the sum of terms formula is,

`Sn=(n)/(2)\lbrack2a+\mleft(n-1\mright)d\rbrack`

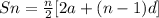
So substituting we get,

`\begin{gathered} Sn=(n)/(2)\lbrack2a+(n-1)d\rbrack \\ S_(20)=(20)/(2)\lbrack2*25+(20-1)(-3)\rbrack \\ S_(20)=10\lbrack50+(-3)(19)\rbrack \\ S_(20)=10\lbrack50-57\rbrack \\ S_(20)=10\lbrack-7\rbrack \\ S_(20)=-70 \end{gathered}`

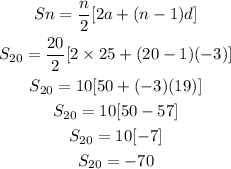
So the sum of terms is -70.