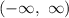Question

Hello, May I please get some assistance with this homework question? I posted an image below Q3

Answer 1

The functions f(x) and g(x) are defined as:

`\begin{gathered} f(x)\text{ = }(3)/(x-7) \\ g(x)\text{ =}(1)/(x) \end{gathered}`

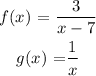
Let us begin by defining a composite function

Function composition is an operation ∘ that takes two functions f and g, and produces a function h = g ∘ f such that h(x) = g(f(x)).

a) f o g:

`\begin{gathered} (f\text{ o g)(x) = }\frac{3}{(1)/(x)\text{ -7}} \\ =\text{ }(3)/((1-7x)/(x)) \\ =\text{ }(3x)/(1-7x) \end{gathered}`

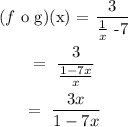
The domain is the set of allowable x-values. Since the function is rational, the values of x that would make the function undefined can be obtained by setting the denominator to zero:

`\begin{gathered} 1-\text{ 7x = 0} \\ 7x\text{ = 1} \\ x\text{ = }(1)/(7) \end{gathered}`

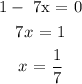
Hence, the domain using interval notation is:

`(-\infty\text{ , }(1)/(7))\text{ U (}(1)/(7)\text{ , }\infty)`

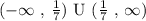
b) g o f:

`\begin{gathered} (g\text{ o f)(x) = }(1)/((3)/(x-7)) \\ =\text{ }(x-7)/(3) \end{gathered}`

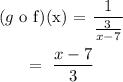
The domain is:

`(-\infty,\text{ }\infty)`