To answer this, we have to use the conservation of momentum law, which indicates that the sum of initial momentums is equal to the sum of final momentums after a collision.
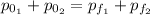
Using the definition of momentum p = mv, we have
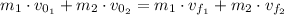
Replacing the given information, we have
![1\operatorname{kg}\cdot5m/s+3\operatorname{kg}\cdot2m/s=1\operatorname{kg}\cdot4m/s+3\operatorname{kg}\cdot v_(f_2)]()
Then, we solve for the final velocity of the heavier car
![\begin{gathered} 5\operatorname{kg}\cdot m/s+6\operatorname{kg}\cdot m/s=4\operatorname{kg}\cdot m/s+3\operatorname{kg}\cdot v_(f_2) \\ 11\operatorname{kg}\cdot m/s-4\operatorname{kg}\cdot m/s=3\operatorname{kg}\cdot v_(f_2) \\ 7\operatorname{kg}\cdot m/s=3\operatorname{kg}\cdot v_(f_2) \\ v_(f_2)=\frac{7\operatorname{kg}\cdot m/s}{3\operatorname{kg}} \\ v_(f_2)\approx2.3m/s \end{gathered}]()
Hence, the final speed of the 3.0 kg cart is 2.3 m/s, approximately.