We are given the graphs of two functions f(x) and g(x) and we are asked to determine the following operations:
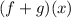
Part (a): To determine the sum of the two functions we need to have into account the sum of two functions is given by the following relationship:
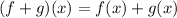
Since we are required to determine this value at x = -2 we replace "x" in the functions for -2:
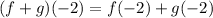
Therefore, we need to determine the values of f(-2) and g(-2), we do this using the corresponding graphs. From the graphs we obtained to values:
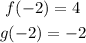
We obtained them like this:
Now we replace these values and we get:
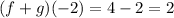
Therefore, the sum of the functions is 2.
Part (b). We are asked to determine the following:

We use a relationship similar to the previous one:
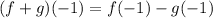
Now we determine the values of f(-1) and g(-1) from the graph and we get:
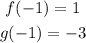
In the graph it looks like this:
Now we replace the values and we get:

Therefore, the difference of the function at x = -1 is 4.
Part (b): We are asked to determine the production of the function at x = 0. We use the following relationship:
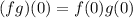
Now we determine the values of the function at x = 0:
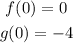
In the graph it looks like this:
Replacing the values we get:
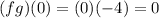
Part (d). we are asked to determine the composition of the two functions at x = 0. To do that we use the following relationship:
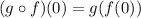
Therefore, we need first to determine the value of f(0) and then evaluate g(x) at that value. The value of f(0) we obtained it in point C and it is:
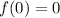
Replacing this value we get:
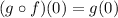
Now we use the value of g(0) that we got in point C:
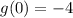
therefore, the composition is:

Part E: We are asked to determine the quotient between the two functions:

We use the values of the functions at x = -1 that we determined in part B. those values are:
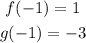
Replacing the values:

Therefore, the quotient of the functions is -1/3.