Question

A(find the vertex of the parabolab)is the vertex a minimum or a maximum

Answer 1

The equation of a parabola in vertex form is given by:

`y=a(x-h)^2+k`

where h and k are the coordinates of the center of the vertex

The given equation

`y=2x^2+4x-5`

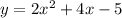
can be expressed in vertex form by following the steps:

Step1: factor out 2 to get a

`y=2(x^2+2)-5`

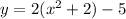
Step2: find the square of half of 2

`\Rightarrow1^2`

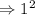
Step 3: Re-write the equation

`\begin{gathered} y=2(x^2+2+1^2)-1^2-5 \\ y=2(x+1)^2_{}-1^2-5 \end{gathered}`
`y=2(x+1)^2-6`

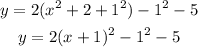
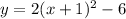
Thus the equation of the vertex is

`\begin{gathered} y=2(x+1)^2-6 \\ \end{gathered}`

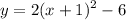
If we compare this with the equation of a parabola in vertex form

`\begin{gathered} a=2 \\ h=-1 \\ k=-6 \end{gathered}`

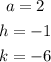
From the values given

Part A

The vertex of the parabola is

`\begin{gathered} \Rightarrow\text{ (-1,-6)} \\ \Rightarrow h=-1,\text{ k=-6} \end{gathered}`

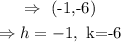
Part B

From the equation

a=2

Since the value of a is a positive, The vertex is a minimum