The gravitational force acting on the mass is,
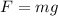
The spring constant of the spring can be given as,
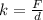
Substitute the known expression,
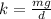
Substitute the known values,
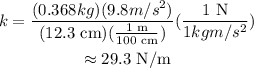
The work done to stretch the spring is,
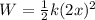
Here, x is the amount of spring stretched in part (b).
Substitute the known values,
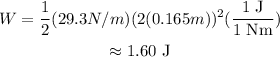
Thus, the work done to stretch the spring is 1.60 J.