Step-by-step explanation: As we can see we are dealing with a monthly compound interest problem so we will need to use the following formula
Step 1: Once we have two different cards we will have two different equations following the formula above. Now let's identify the value of the variables for each card as follows.
- Card A: P = there is no information
r = 12.5%/100% = 0.125
t = 1 year
n = 12 monsths
- Card B: P = there is no information
r = 15.49%/100% = 0.1549
t = 1 year
n = 12 months
Step 2: There is still additional information we need to consider before building our expressions. Card A has an annual fee of $48 which means we need to add this value to our expression. On the other hand Card B has no annual fee which means our expression remains unchanged.
Step 3: Now we are able to substitute the values and build the expressions for Card A and B. Also, once we need to know "the amount at which the cards offer the same deal over the course of a year" we will make both equations equal as follows
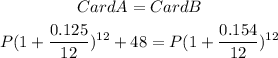
Final answer: As we can see above the final answer is the letter D.