Answer:
73
Step-by-step explanation:
The average rate of change for the function g(x) between a and b can be calculated as:
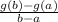
So, if a = 3 and b = 7, we first need to calculate g(3) and g(7):
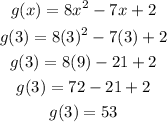
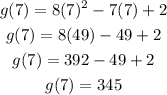
Now, the average rate of change is equal to:
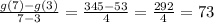
Therefore, the average rate of change of g(x) between 3 and 7 is 73.