See graph below
Step-by-step explanation:

From the equation, the highest point of the graph = -0.5
y = -0.5
To p;ot the graph, we can ssign values for x, inorder to get corresponding y values
let x = -3π/2, 0, 3π/2
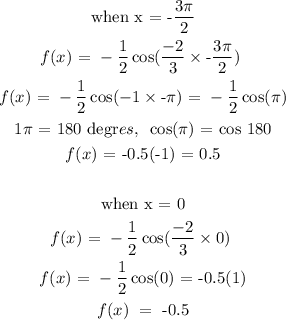
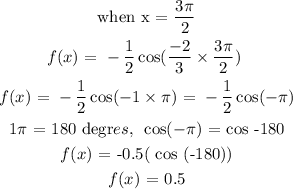
Plotting the graph:
This graph doesn't have the same readings in its x axis as the graph you attached. It is meant as a guide on how the curve should look like
plotting the points on the given graph (sketch):