Question

The equation V =34300 (0.93 ) t V= 34300 (0.93) t represents the value (in dollars) of a car t years after its purchase.

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Write the given exponential function

`V=343000(0.93)^t`

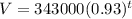
STEP 2: Explain the standard exponential function

`\begin{gathered} y=ab^x \\ \text{where }b\text{ is the base of the function} \end{gathered}`

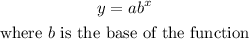
STEP 3: Explain when an exponential function increases and decreases

If the base b is greater than 1, then the function increases exponentially at a growth rate of b. This is known as exponential growth.

If the base b is less tha 1 but greater than zero, the function decreases exponentially at a rate of

b. This is known as exponential decay.

STEP 4: Compare the given value of b for the function in step 1

Since the value of b in the function is less than 1 but greater than 0, i.e, 0.93, hence, the value of the car is decreasing at a rate of dollars per year.

The purchase price of the car was 34300 dollars since that was the initial value of a.