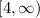Question

For the real values functions f(x) = x + 5 and g(x) = Vx-4, find the composition f g and specify its domain using interval notation.be(2) -

Answer 1

The given functions are

`\begin{gathered} f(x)=x^2+5 \\ g(x)=\sqrt[]{x-4} \end{gathered}`

We need to find the composite function f(g(x))

Which means, replace x in f(x) by g(x)

`f(g(x))=(\sqrt[]{x-4})^2+5`

Power 2 will cancel the square root

`\begin{gathered} f(g(x))=x-4+5 \\ f(g(x))=x+1 \end{gathered}`

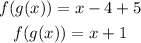
Let us find the domain of f(g(x))

Since there is no square root for a negative number, then

`x-4\ge0`

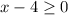
Add 4 to both sides, then

`\begin{gathered} x-4+4\ge0+4 \\ x\ge4 \end{gathered}`

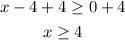
Then the domain of f(g(x)) should be

`\lbrack4,\infty)`