Question

The entry ticket for a Science Exhibition is $5 for students and four dollars more than the students for adults. On a particular day, 600 people visited the exhibition and $3500 was collected. How many students and adults visited on that day?

Answer 1

Given:

Entry ticket for students = $5

Entry ticket for adults = $5 + $4 = $9

Number of people = 600

Total amount collected = $3500

Let's find the number of students and adults who visited on that day.

Let S represent the number of students and A represent the number of adults.

We hav the system of equations:

5S + 9A = 3500

S + A = 600

Let's solve the system of equations simultaneously using substitution method.

Rewrite the second equation for S:

S = 600 - A

Substitute (600 - A) for S in the first equation:

`\begin{gathered} 5(600\text{ - A\rparen + 9A}=\text{ 3500} \\ \\ \text{ Apply distributive property:} \\ 5(600)+5(-A)+9A=3500 \\ \\ 3000-5A+9A=3500 \\ \\ 3000+4A=3500 \\ \\ 4A=3500-3000 \\ \\ 4A=500 \end{gathered}`

Divide both sides by 4:

`\begin{gathered} (4A)/(4)=(500)/(4) \\ \\ A=125 \end{gathered}`

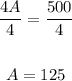
Substitute 125 for A in either of the equations:

`\begin{gathered} S=600-A \\ \\ S=600-125 \\ \\ S=475 \end{gathered}`

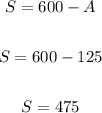
Therefore, we have the solutions:

S = 475, A = 125

Therefore, the number of students that visited is 475 while the number of adults is 125 .

ANSWER:

Students = 475; Adults = 125