Question

On a 20 problem test, how many ways can a person get 4 problems correct and 16 problems wrong?

Answer 1

This is a combination problem where the order doesn't matter.

We compute the number of combinations with the following formula:

`C^{n_{}}_r=(n!)/(r!(n-r)!)`

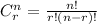
Where n is the number of things to choose from, and we choose r of them. No repetition, the order doesn't matter.

In our problem, we have n = 20 and for r we can pick r = 16 or r =4 (with both options we get the same result), picking r = 16 we get:

`C^{20_{}}_(16)=(20!)/(16!\cdot(20-16)!)=(20!)/(16!\cdot4!)=4845`

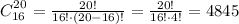
Answer

We have 4845 ways possible to get 4 problems correct and 16 problems wrong from a 20 problem set.