Question
Step-by-step explanation
we are given the height function as:
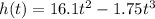
The first step will be to get the velocity function
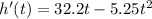
The acceleration is given by
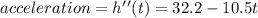
Since we are told to find how high the rocket will be at an instant of 10ft/s²
Therefore, we will equate the acceleration formula to 10ft/s² so that we will obtain t
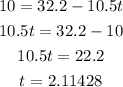
The final step will be to substitute t =2.11428 into the initial height function
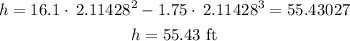
The answer is h = 55.43 ft
Part F
was when the rocket is moving 35ft/s, we will have to equate 35ft/s into the velocity formula
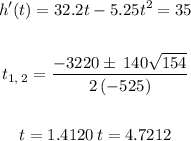
But we are told that t cannot be greater than 4
So that t=4.7212s is invalid
Thus, our value for t= 1.4120
So we will substitute this to get the acceleration
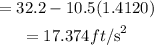
The answer is 17.37 ft/s²