Question

The following statement is not true by mathematical induction:1 + 3 + 5 + ... + (2n - 1) = n2 for all natural numbers n.TrueFalse

Answer 1

We are given the following succession:

`1+3+5+\cdots+(2n-1)=n^2`

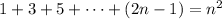
To prove this by mathematical induction we need first to determine if the statement is true for n = 1. Replacing we get:

`\begin{gathered} 1=1^2 \\ 1=1 \end{gathered}`

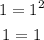
Therefore, the statement is true for n = 1. Now we will assume that the statement is true and see if it holds for n + 1

Replacing n + 1: