Question

a certain rectangular prism has a height of 6m a length of 5 m and a width of 4M give the dimensions of a second rectangular prism that will have the same surface area as the first one.

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Write the given sides of the first rectangular prism

`h=6m,l=5m,w=4m`

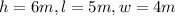
STEP 2: Write the formula for calculating the surface area of the first rectangular prism

`\text{Surface area=}2\left(lw+lh+hw\right)`

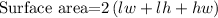
STEP 3: Caclulate the surface area of the first rectangular prism

`\begin{gathered} Surface\text{ area=}2\left\lbrack\left(5*4\right)\right?+\left(5*6\right)+\left(6*4\right) \\ surface\text{ area=2\lparen20+30+24\rparen=2\lparen74\rparen=148} \\ \\ \therefore surface\text{ area}=148m^2 \end{gathered}`

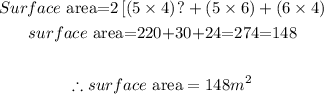
STEP 4: Give the dimensions of a second recatngular prism that will have same surface area

We assume three dimensions that will give same 148 squared meter for the second rectangular prism

`\begin{gathered} Suppose;l=11,w=4,S.A=148m^2 \\ \\ we\text{ solve for h} \\ Using\text{ the formula in step 2} \\ S.A=2\left(lh+lw+hw\right) \\ 148=2\left\lbrack\left(11h)+\left(11*4\right)+\left(4h\right)\right)\right? \\ 148=2\left(15h+44\right) \\ Divide\text{ both sides by 2} \\ (148)/(2)=15h+44 \\ 74=15h+44 \\ Subtract\text{ 44 from both sides} \\ 74-44=15h+44-44 \\ 30=15h \\ Divide\text{ both sides by 15} \\ (30)/(15)=(15h)/(15) \\ 2=h \\ h=2 \end{gathered}`

Hence, the dimensions of the second rectangular prism that will have the same surface area are:

length = 11m

width = 4m

height = 2m