cleThe given region is a semicircle with a radius DQ=10''.
It is required to find the exact perimeter and the exact area.
(a) Recall that the perimeter of a semicircle is the sum of half of the circumference of the circle and its diameter:
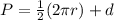
Note that the diameter is twice the radius, that is, d=2r.
Hence, the perimeter becomes:
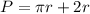
Substitute r=10 into the formula:
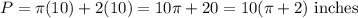
The exact perimeter of the region is 10(π+2) inches.
(b) The Area of a Semicircle is half the area of a circle given as:
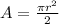
Substitute r=10 into the formula:

The exact area of the region is 50π square inches.
Answers:
The exact perimeter of the region is 10(π+2) inches.
The exact area of the region is 50π square inches.