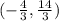Given the inequality:
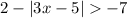
To find x, follow the steps below.
Step 01: Isolate the absolute value.
To do it, first, subtract 2 from both sides of the inequality.
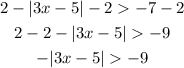
Now, multiply the equation by -1:
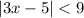
If |3x - 5| < 9, then 3x - 5 < 9 or -(3x - 5) < 9.
Step 02: Find the interval in which 3x - 5 < 9.

Isolate x by adding 5 to both sides. In sequence, divide the sides by 3:
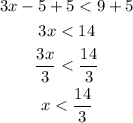
Step 03: Find the interval in which -(3x - 5) < 9.
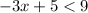
To isolate x, first, subtract 5 from both sides. Second, divide the sides by 3. Finally, multiply the inequality by -1.

Step 04: Graph the interval.
Since x < 14/3 and x > -4/3:
Graphing the answer:
Step 05: Write your answer in interval notation.
/(3),(14)/(3))](https://img.qammunity.org/2023/formulas/mathematics/high-school/v9hfnr09et1hrzawxndd1noumkygs33fxc.png)
Step 06: Double-check the solution.
To double-check the solution, choose one point inside the interval and observe if the answer fits the equation. You can also choose a point outside the interval.
Let's choose x = 0 (inside the interval) and x = 5 (outside the interval).
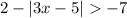
Substituting x by 0.
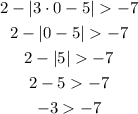
True.
Substituting x by 5.
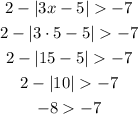
False, since -8 is not greater than -7. It is expected since 5 is not an answer for this inequality.
Answer: