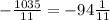Question

What number is missing to make the following statement true? 8/11=7 ?/15

Answer 1

First we need to rewrite the mixed number (7 ?/15)​ on the right of the equation as a fraction, we can do it like this:

1. multiply the whole number part (7) by the fraction's denominator

7 * 15 = 105

2. Add that to the numerator (?)

105 + ?

3. write the result on top of the denominator

(105 + ?)/ 15

Now that we converted the mixed number on the right side, we can rewrite the equation like this:

8/11 = (105 + ?)/ 15

From this expression, we can solve for ? by following these steps:

1. multiply both sides of the equation by 15:

`\begin{gathered} (8)/(11)*15=((105+?))/(15)*15 \\ (8*15)/(11)=(105+?)*(15)/(15) \\ (120)/(11)=(105+?)*1 \\ (120)/(11)=105+? \end{gathered}`

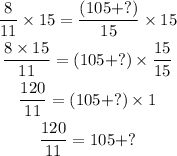
2. Subtract 105 on both sides:

`\begin{gathered} (120)/(11)=105+? \\ (120)/(11)-105=105-105+? \\ (120)/(11)-105=0+? \\ (120)/(11)-105=? \end{gathered}`

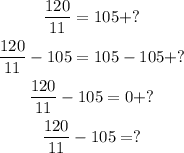
3. Solve the subtraction on the left side by multiplying and dividing 105 by 11:

`\begin{gathered} (120)/(11)-(105*11)/(11)=? \\ (120)/(11)-(1155)/(11)=? \\ ?=(120-1155)/(11) \\ ?=(-1035)/(11) \end{gathered}`

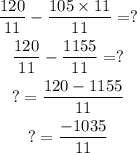
Then, ? is:

`-(1035)/(11)=-94(1)/(11)`