Given the above composite figure, its surface area is evaluated to be the sum of the surface area of each of its plane surfaces.
Step 1:
Thus, the surface area of the figure:
![=\text{area of ABCD + area of CDE + area of FGJ + area of GHIJ + area of BDGH + area of ACJI + area of EFDG + area of CEFJ + area of ABHI}]()
The surface area of ABCD:
ABCD takes the shape of a rectangle. The area of a rectangle is given as
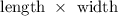
Thus, the surface area of ABCD is calculated as
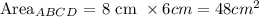
The surface area of CDE:
CDE takes the shape of a triangle. The area of a triangle is given as
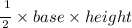
Thus, the surface area of CDE is calculated as
![\text{Area}_(CDE)=(1)/(2)*8\operatorname{cm}\text{ }*3cm=12cm^2]()
The surface area of FGJ:
FGJ has the same shape and dimension as CDE. Thus, the surface area of FGJ is 12cm²
The surface area of GHIJ:
GHIJ has the same shape and dimension as ABCD. Thus, the surface area of GHIJ is 48cm².
The surface area of BDGH:
BDGH takes the shape of a rectangle. Thus, its area will be
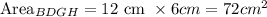
The surface area of ACJI:
ACJI has the same shape and dimension as BDGH. Thus, its area will be 72 cm²
The surface area of CEFJ:
CEFJ has the shape of a rectangle. Its area will be calculated as
![\begin{gathered} \text{Area}_(CEFJ)=\text{ 8cm }*5\operatorname{cm} \\ =40\operatorname{cm}\text{ squared} \end{gathered}]()
The surface area of EFGD:
Since EFGD has a similar shape and dimension as CEFJ, its area will as well be 40 cm²
The surface area of ABHI:
ABHI has the shape of a rectangle. Thus, its area will be
![\text{Area}_(ABHI)=12\operatorname{cm}*8\operatorname{cm}=96\operatorname{cm}\text{ squared}]()
Step 2:
Sum the surface area of all plane surfaces of the composite figure
![\begin{gathered} (48+12+12+48+72+72+40+40+96)cm^2 \\ =440\operatorname{cm}\text{ squared} \end{gathered}]()