Question

Solve the triangle if possible, givenA=30° a=8 b=16

Answer 1

We have two sides of the triangle (a=8 and b=16) and an angle (30°).

We will assume that the known angle is between the known sides a and b.

We can start by calculating the third side "c" with the Law of cosines:

`\begin{gathered} c^2=a^2+b^2-2ab\cdot\cos (A) \\ c^2=8^2+16^2-2\cdot8\cdot16\cdot\cos (30\degree) \\ c^2=64+256-256\cdot\frac{\sqrt[]{3}}{2} \\ c^2=320-128\sqrt[]{3} \\ c^2\approx320-221.7 \\ c\approx\sqrt[]{98.3} \\ c\approx9.9 \end{gathered}`

Now, we can use the Law of sines, where the quotient between the sine of an angle and its opposite side is constant for each of the angles:

`(\sin(A))/(c)=(\sin (B))/(a)=(\sin(C))/(b)`

We already know the value of the first term:

`(\sin(A))/(c)=(\sin (30\degree))/(9.9)=(0.5)/(9.9)=(5)/(99)`

Then we can calculate the measure of B as:

`\begin{gathered} \sin (B)=a\cdot(\sin(A))/(c)=8\cdot(5)/(99)\approx0.404 \\ B=\arcsin (0.404) \\ B\approx23.8\degree \end{gathered}`

Now we can calculate the measure of C as:

`\begin{gathered} A+B+C=180\degree \\ 30+23.8+C=180 \\ C=180-30-23.8 \\ C=126.2\degree \end{gathered}`

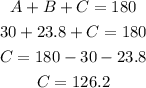
Answer:

The sides of the triangle are: 8, 16 and 9.9.

The angles of the triangle are: 30°, 23.8° and 126.2°.