Explanation
We are given the following:
• A certain train has 10 cars that are lined up on a track.
,
• One of the cars is the engine.
,
• Another is a caboose.
,
• The engine will be first in line.
,
• The Caboose will be the last car in line.
We are required to determine the number of ways can the cars be lined up.
We know that there are 10 cars of which two will be the engine and the caboose. Hence,
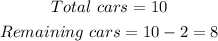
We also know that these problems deal with the arrangement of the cars. Therefore, we will use permutation to determine the number of ways as follows:
![\begin{gathered} ^nP_r=(n!)/((n-r)!) \\ n=8\text{ }[number\text{ }of\text{ }spaces\text{ }available] \\ r=8\text{ }[number\text{ }of\text{ }cars\text{ }left] \\ \therefore^8P_8=(8!)/((8-8)!)=(8!)/(0!) \\ where\text{ }0!=1 \\ \Rightarrow^8P_8=(8!)/(1)=8!=40,320\text{ }ways \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/9cofqnywtcfeauorlzy6zxzyw8rmjz4vpx.png)
Hence, the cars can be lined up in 40,320 ways.