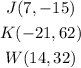Question

Which of the following represents a rotation of JKW, which has vertices J (-7, 15), K (21, -62), and W (-14 , -32), about the origin 180"?

Answer 1

The fourth option:

J(7, - 15)

K ( -21, 62)

W(14, 32)

Step-by-step explanation:

The counterclockwise rotation by 180 degrees about the origin corresponds to the following transformation of coordinates.

`(x,y)\to(-x,-y)`

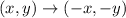
This means that if we have the point J (-7, 15), then under 180 counterclockwise rotation about the origin, it transforms to

`\begin{gathered} J(-7,15)\to J(--7,1-5) \\ \to J(7,-15) \end{gathered}`

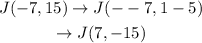
Similarly, the point K(21, -62) transforms to

`K\mleft(21,-62\mright)\to K(-21,62)`

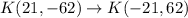
and

`W(-14,-32)\to W(14,32)`

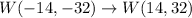
Hence, to summerise, a 180-degree counterclockwise rotation about the origin brings about the following changes

`\begin{gathered} J\mleft(7,-15\mright) \\ K(-21,62) \\ W\mleft(14,32\mright) \end{gathered}`