let's start by drawing a diagram of the situation
In order to find the magnitud of the resulting force we need to find the forces towards the west direction
Then
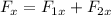
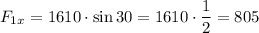
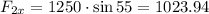
Thus,
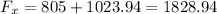
In the y axis we have:
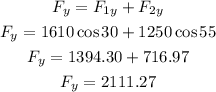
Then, finally, we add both forces as follows
![F=\sqrt[]{(F_x)^2+(F_y)^2_{}}_{}](https://img.qammunity.org/2023/formulas/mathematics/college/c65423o2dnwfn1aihzjva063kwxthshnp0.png)
replacing
![\begin{gathered} F=\sqrt[]{1828.94^2+2111.27^2} \\ F=2793.29 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/bmj9ufsz3iv69a8oqal7o0m7tuwtniqqve.png)
Then the magnitud of the resulting forces in x and y directions is: 2793.29 kg