1 Answer

Myron · Answer 1 · 2023-11-12T06:30:27+0000

Substitute 221 for V in the formula

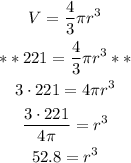
$\begin{gathered} V=(4)/(3)\pi r^3 \\ \ast\ast221=(4)/(3)\pi r^3\ast\ast \\ 3\cdot221=4\pi r^3 \\ (3\cdot221)/(4\pi)=r^3 \\ 52.8=r^3 \end{gathered}$

So the radius of the ball is

$\begin{gathered} 52.8cm^3=r^3 \\ \sqrt[3]{52.8cm^3\text{ }}=r \\ \ast\ast3.75cm=r\text{ }\ast\ast \end{gathered}$

The base of the cylindrical package will a radius equal to that of the tennis ball, or

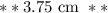
$\ast\ast3.75\text{ cm }\ast\ast$

The height of the package will equal the diameter of three tennis balls, or

$\begin{gathered} \ast\ast3\lbrack2(3.75cm)\rbrack\ast\ast=\ast\ast3\lbrack7.5cm\rbrack\ast\ast=\ast\ast22.5\operatorname{cm}\ast\ast \\ \end{gathered}$

This is because the diameter is twice the radius and we have 3 tennis balls in the cylindrical package.

So, the volume of the package is

$\begin{gathered} V=\pi r^2h \\ V=\ast\ast\pi(3.75cm)^2\ast\ast\cdot\ast\ast22.5\operatorname{cm}\ast\ast \\ V=\ast\ast316.41\ast\ast\operatorname{cm}^3 \end{gathered}$

And since we are asked to round to the next cubic centimeter, then the volume of the cylindrical package is

$V=316\operatorname{cm}^3$

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

0 Comments

Please log in or register to add a comment.

Other Questions