Given:
The initial velocity, u=0 m/s
The acceleration during the 1st interval, a₁=2.60 m/s²
The time duration of the 1st interval, t₁=14.0 s
The time duration of the second interval, t₂=3.00 min=180 s
The acceleration during the 2nd interval, a₂=0 m/s²
The acceleration during the 3rd interval, a₃=-9.45 m/s²
The time duration of the 3rd interval, t₃=3.85 s
To find:
a) The total displacement of the trip.
b) The average velocities.
Step-by-step explanation:
a)
The final velocity of the 1st interval is the constant velocity during the 2nd interval. This is also equal to the initial velocity of the third interval.
And it is given by,
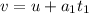
On substituting the known values,
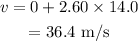
From the equation of motion, the total distance covered during the 1st interval is given by,
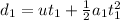
On substituting the known values,
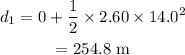
The distance traveled in the 2nd interval is given by,

On substituting the known values,
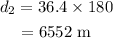
From the equation of motion, the distance covered during the 3rd interval is given by,

On substituting the known values,
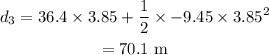
Thus the total displacement of the trip is,
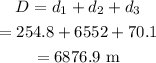
b)
The average speed is given by,
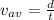
Thus the average speed for 1st leg is,
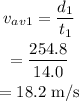
The average speed for 2 nd leg is,
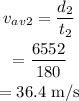
The average speed for 3rd leg is,
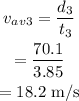
Thus the average speed of the complete trip is given by,
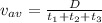
On substituting the known values,

Final answer:
a) The total displacement of the trip is 6876.9 m
b)
The average speed for 1st leg is 18.2 m/s
The average speed for 2nd leg is 36.4 m/s
The average speed for 3rd leg is 18.2 m/s
The average speed for the complete trip is 34.8 m/s