You have a deck of 20 cards numbered from 1 to 20.
If you draw a card at random, the set of possible outcomes is:
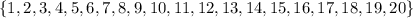
Let "A" represent the event "draw a card at random and it has a number less than 9"
The possible outcomes from the deck that fulfill the condition stated for A are all cards with numbers less than 9:
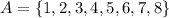
So out of the 20 cards, there are 8 cards with a number "less than 9"
The probability of drawing a card with a number less than 9 can be determined as the quotient between the favourable outcomes and the total number of outcomes:
Favorable outcomes: 8
Total outcomes: 20
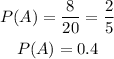
The probability that a card is chosen at random has a number less than 9 is 0.4