Given:
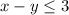
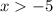
Consider the equation of the first inquality.

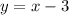
Set x=0, we get
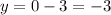
We get the point (0,-3).
Set x=3, we get

We get the point (3,0).
Mark the points (0,-3) and (3,0) and draw a ray to join the points.
Let a point (0,0) from the left of the line that does not lie on the line.
substitute x=0, y=0 in the given inequality, we get
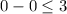
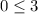
This is true so the point from the left side of the equation line on the inequality.
Now shade the left side of the line.
The next inequality is
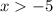
Draw a dotted vertical line that parallels the y-axis at the point (-5,0).
And the values are greater than -5, so shade the right side of the line.
The graph is
The intersection of the coordinates is the grey shaded region.
The whole region lies between (-5,0),(-5,-8), (0,-3) and (3,0).
We can see that (0,0) is also the intersection of the given inequalities.