The equation is given as ;
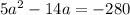
Divide both terms by 5 as;
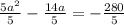
This will give the following;
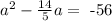
Find { b/2}^2 and add it on both sides of the equation where b is the second term in the equation.
{-14/5 / 2 }^2 = {-14/5 * 1/2 }^2 = {-14/10}^2 = {-7/5}^2 = 49/25
Add this on both sides of the equation as;
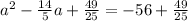
Factorize as ;
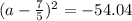
From the above, you notice, a square-root of a negative number will not result to real solutions for a, thus; the equation has no real solution.
Answer:
No real solution