Given the following Quadratic equation:
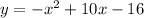
1. You can find the vertex as following:
-Find the x-coordinate of the vertex with this expression:
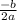
In this case:

Then, substituting values, you get:
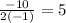
- Substitute this value into the Quadratic equation and evaluate, in order to find the y-coordinate of the vertex. This is:

Then, the vertex is:
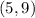
2. Now let's find the roots:
- Substitute the following value of "y" into the equation:

Then:
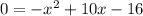
- In order to make the leading coefficient positive, multiply both sides of the equation by -1:
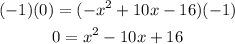
- Factor the equation. Find two numbers whose sum is -10 and whose product is 16. These would be -8 and -2. Then:
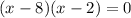
- The roots are:
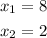
3. Now let's find five points to plot them in the coordinate plane. Give five different values to "x" and evaluate in order to find the corresponding value of "y". Then:
- When
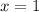
You get:
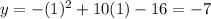
The point is:
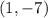
- When

You get:
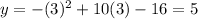
The point is:
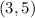
- When:

You get:
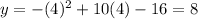
The point is:
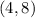
- When:
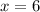
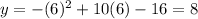
The point is:
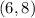
- When:
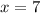
You get:
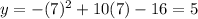
The point is:

Finally, you get the following graph of the equation: